If you’ve ever encountered the distributive property formula in math class, then you’re already familiar with one of its more important applications: distributing sums of fractions among multiple terms. The distributive property can also be used to simplify complex algebraic equations, and it’s even been shown to be helpful for problem solving in other areas of mathematics. In this article, we’ll explore what the distributive property is, and how it can help you solve problems.
What is the distributive property example?
The distributive property is a mathematical equation that states that for every number of substances, there is a corresponding number of mixtures. For example, if there are three substances, there will be 3×2=6 mixtures. The distributive property can also be used to determine the total amount of a certain substance when mixed with other substances.
What property is distributive property?
The distributive property states that if a property is distributive, then each member of a group possessing the property also possesses it. An example of the distributive property is that if x + y = z, then x + (y+z) also equals z.
The distributive property can be seen as an extension of the addition and multiplication properties. The distributive property states that if two properties are distributive, then their combined effect is also distributive. For instance, the distributive property states that if x + y = z, then x + (y+z) = (x+y)+(z+z).
What is the distributive property formula?
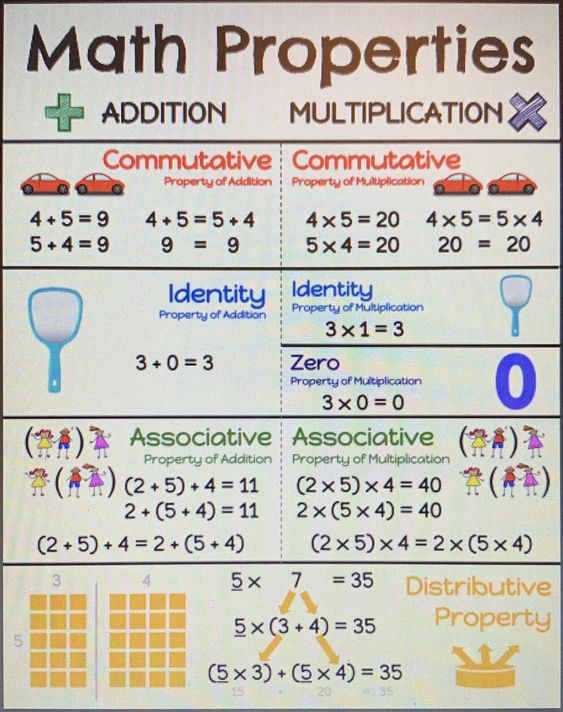
The distributive property formula states that if you divide a number among several different items, each item will get an equal share. For example, if you divide 24 by 3 students, each student will get 6 pieces of candy.
What is distributive property short answer?
The distributive property states that if you have a set of items, each of which can be distributed among multiple individuals, then the total amount of items distributed will be the same as the total number of items in the set.
For example, if you have 10 rocks and want to distribute them between 3 people, the rocks will be distributed among the 3 people. If you have 12 rocks and want to distribute them between 5 people, then the rocks will be distributed among the 5 people. The total number of rocks distributed will be 18.
What is the distributive property 3rd grade math?
The distributive property is a simple mathematical formula that you may use when dividing numbers. It states that if you divide two numbers, the result will be the same as if you divide the smaller number by the larger number. For example, if you divide 3 by 2, the result will be 1.5. This is also true for other multiplication and division operations.
There are three main rules for applying the distributive property:
Rule 1: If you have a group of things (like parentheses), the distributive property applies to each element in the group separately.
For example, if you have (3 + 2) ÷ (5 – 4), the answer is 9 because 3 + 2 is 13 and 5 – 4 is 3. (3 + 2) ÷ (5 – 4) equals 9 because 3 + 2 is 13 and 5 – 4 is 3.)
Rule 2: The distributive property also applies to negative numbers. In other words, if you have -3 + 2, the answer would be -1 because 3 + 2 is 5 and -3 + 2 is 7. (3 + 2) ÷ (-3 + 2) equals 1 because 3 + 2 is 5 and
How do you do distributive property in multiplication?
The distributive property is a mathematical concept that states that if you have an equation with two variables, then each variable is distributed according to the distributive property. This means that each term in the equation will be distributed according to the rules of multiplication.
The distributive property can be applied to multiplication problems, but it’s important to remember the order of operations when working with it. The order of operations is: Parentheses, Exponents, Multiplication and Division (from left-to-right), like this: 3x(4y+5) = 9.
When working with distributive property problems, it’s important to keep these basic rules in mind:
One key rule for the distributive property is that you must distribute the exponents (ie. raise them all to the same power). This is why 3x(4y+5) = 9, because x = 3, y = 4, and 5 is raised to the power of both x and y.
Another important rule for the distributive property is that you must distribute the parentheses evenly. For example, (3x+4)y = 10 because 3x+4 goes inside the
How do you explain distributive property to a child?
Distributive property is a mathematical principle that states that if you have a set of objects, and each object has a number of properties, then the total number of properties possessed by the set is equal to the sum of the numbers of properties possessed by each object in the set. For example, if John has two apples and Mary has three apples, then John has four properties and Mary has six properties.
How do you do the distributive property step by step?
The distributive property is one of the most important formulas in mathematics. It allows you to do basic arithmetic problems with many variables, without having to remember how to do multiplication and division.
The distributive property is also known as the additive property, because it simply states that if you add together like terms in a group (such as 3 + 4), the result is always the sum of the individual like terms (7).
Here’s an easy way to remember how to do the distributive property:
If there are two or more variables in a problem, place them in parentheses and list them from left to right. The distributive property will tell you what operation to apply to each variable in the parentheses.
For example, in the problem 5 + (3x + 2y), 5 goes into (3x + 2y) first, then is added to 5 again, and finally 2y goes into it. So 5 + (3x+2y) = 10.
Here are some examples of problems that use the distributive property:
-5x + 6y = 15
-5x(6 – x) = 15
-3a(b – 4
Which number sentence is an example of the distributive property?
The distributive property is an mathematical theorem that states that for any number of items, the total amount of each item is the same. An example of the distributive property is “The total amount of candy given out is the same for each child.”
What does distributive mean in math?
The distributive property, also known as the distributive law, states that for any number of objects, a function will distribute the total amount of work evenly among the objects.
For example, if you have eight candy bars and want to share them equally with your friends, you can divide the candy bars among your friends using the distributive property. Each friend would get three candy bars.
Which one is an example of distributive law?
The distributive property is an example of distributive justice. It states that if you distribute something evenly among a group, each person will receive the same amount.
What is an example of distributive property of addition?
One example of the distributive property of addition is when 3 + 4 = 7. The 3 gets distributed to the 4, and then the 7 is created.
distributive property table
The distributive property is one of the most important mathematical concepts. It states that for every number there is a unique combination of things that can be done with that number. The distributive property can be used to solve equations and problems.
The distributive property is simple to remember. It states that if you have two or more numbers, and you want to do something with each number, you can divide the numbers into groups and then do the thing with each group.
There are three general rules for the distributive property:
The distributive property always works.
The distributive property applies to addition, subtraction, multiplication, and division (but not division by zero).
There is an order to how the properties work.
distributive property of addition
The distributive property of addition is a mathematical law that states that for any number of things, the total amount of each thing is the sum of the amounts of the individual things.
For example, if there are three candy bars and five ants, then the total amount of candy is six. The three candy bars add up to three, and the five ants add up to fifteen.
distributive property formula
The distributive property states that if x is a number and y is a number, then x + y is also a number. For example, if John has 3 apples and gives 2 away to Bob, then John has 4 apples. The distributive property can be summarized in three steps:
Step 1: identify what properties need to be satisfied
In the example above, the distributive property needs to be satisfied because x must be a number and y must be a number.
Step 2: write down the equation for each property
In the example above, the equation for the left side of the distributive property is (x + 2) = 4 and the equation for the right side is (y + 1) = 3.
Step 3: solve for x and y
In the example above, x = 3 and y = 1.
distributive property calculator
The distributive property is a mathematical formula that relates the distributive property to multiplication and division. It states that if a property applies to a set of elements, it also applies to the individual elements. The distributive property can be applied to fractions, decimals, and whole numbers.
The distributive property follows the ordering of operations:
For example, if you have three candy bars and want to share them equally with your friends, you would give each friend one candy bar. If there are five people in your group, then you would give each person two candy bars.
distributive property of multiplication
The distributive property of multiplication states that for every number, there is a unique way to distribute the product of that number and another number. This can be represented by the following equation:
P(x, y) = P(x) * P(y)
For example, if you have 3 balls and want to distribute them equally between two people, you would use the distributive property to do so. First, divide 3 by 2 to get 1. Then, multiply that number by each person’s own ball (1 x 1 = 1, 2 x 1 = 2, and 3 x 1 = 3). So for each person, the distribution would look like this:
distributive property division
In math, there is a distributive property that says that if you divide one number between two others, the result is always the same. The distributive property is represented by the symbol ” distributive “. The distributive property can be very useful when working with fractions and decimals.
The distributive property can be summarized in three steps:
1. Find the total of the numbers divided
2. Find the total of the numbers left over after dividing
3. Apply the distributive property to each of these totals.
Let’s take a look at an example. Say you have a group of four students and they each bring in a lunch box. The boxes contain 24 snacks, 12 lunches, and 4 dinners. Each student is responsible for eating 8 snacks and 4 lunches, leaving 16 snacks and 0 lunches to share between the 4 students. According to the distributive property, each student would get 3 snacks and 1 lunch (8 + 4 = 13).

