In this article, we will explore what rational numbers are, their various types, and some of their properties. We will also cover how to find rational numbers using formulas and how to convert between rational and irrational numbers. Finally, we will provide a full guide on how to use rational numbers in your daily life.
What is a rational number in math?
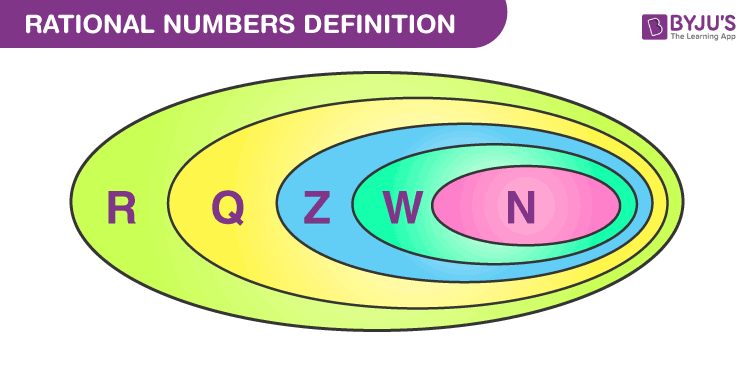
A rational number is a real number that can be expressed as a fraction or a decimal. Rational numbers can be expressed as whole numbers, but they also have properties that make them unique among whole numbers.
There are two types of rational numbers: rational and irrational. Rational numbers are those that can be expressed as fractions or decimals. Irrational numbers are those that cannot be expressed as fractions or decimals.
Some of the properties of rational numbers include the following:
-They can be divided evenly by any whole number without leaving any remainder.
-They add up to 1.
-They are the only type of number that can be expressed as both a fraction and a decimal.
-They have an infinite number of divisors, which means there is a whole number between 1 and itself that can be divided evenly by the number.
What is a rational number example?
A rational number is a number that can be expressed as a fraction or decimal. There are a few specific properties of rational numbers that make them so useful in math and science: they are whole numbers, they are equal if divided by the same number, and they can be represented in any base.
One example of a rational number is 3.141592653589793. This number can be written as a fraction (3/10 or 0.3078125), as a decimal (3.14), or in any base (3, 14, 15, 17). It is also true that 3.141592653589793 is equal to 2 raised to the third power (31.4).
There are other examples of rational numbers too – try practicing calculating some of them out yourself!
Is 2 a rational number?
2 is a rational number. What does that mean? And what are the different types of rational numbers? In this full guide, we’ll explain everything you need to know about rational numbers.
First, let’s look at what rational numbers are. A rational number is a number that can be expressed as a fraction or decimal. For example, 2 is a rational number because it can be written as 20/100 or 2.5.
There are three types of rational numbers: whole numbers, fractions, and decimals. A whole number is something like 2, 3, 5, 7… These are the numbers you’re probably most familiar with. Fractions are like 2/5 or 3/8… These are numbers that have parts like 1/2 or 3/4. Decimals are like .50 or .75… These are numbers that can have hundreds or thousands of zeros after them.
Now that you know what rational numbers are, let’s see how they’re related to other kinds of numbers. A rational number is always equal to another rational number. For example, 2 is equal to 1 + 1/2, 3 is equal to 1 + 1/3, and 5 is
How do you know if a number rational?
What is a rational number?
In mathematics, a rational number is a whole number that can be expressed as a fraction with integer numerators and denominators. In other words, a rational number has an algebraic equation that can be solved using algebraic techniques.
There are many types of rational numbers:
Integers are always rational. That is, they can be expressed as a decimal with no fractions or decimals in the numerator or denominator.
Real numbers are always rational, but they may not be integers. That is, there may be fractions or decimals in the numerator or denominator. For example, 3.141592653589793 is not an integer but 3.1415926535897932 is.
A complex number is also always rational, but it may have fractional components in the numerator or denominator. For example, (1+2i) is irrational but (1+2+3i) is real andrational.
How do you tell if a number is rational or irrational?
There are a few ways to tell if a number is rational or irrational. The most common way is to see if the number can be expressed as a fraction in which the numerator and denominator are both whole numbers. If the number can be expressed as a fraction, it is considered rational. If the number cannot be expressed as a fraction, it is considered irrational.
Another way to tell if a number is rational or irrational is to see if it can be divided by another rational number. If the division by another rational number produces an integer, then the number is considered rational. If the division by another rational number produces a decimal, then the number is considered irrational.
Finally, one can test whether a number is rational or irrational by seeing if it satisfies one of the following properties:
The square root of a negative number is always irrational
The sum of two irrational numbers is always irrational
The product of two irrational numbers is always irrational
Is 0.1875 rational or irrational?
Rational numbers are numbers that can be expressed as a fraction or decimal. They include the numbers 2, 3, 5, 8, and so on.
There are a few things to keep in mind when dealing with rational numbers. First, all rational numbers are square roots of positive numbers. Second, every rational number is the sum of at least two other rational numbers. Finally, all rational numbers have a finite number of digits after the decimal point.
In this guide, we will explore the definition, types, properties, and examples of rational numbers. We will also discuss why 0.1875 is irrational.
Is √ 7 is a rational number?
√7 is a basic arithmetic operation that is used to solve problems. It is also known as the quadratic residue and the cubic root of 7.
What Is a Rational Number?
A rational number is a number that can be expressed as a fraction or as a whole number. For example, 5.6 is a rational number because it can be written as a fraction (5 divided by 2) or as a whole number (5).
What Are the Different Types of Rational Numbers?
There are four different types of rational numbers: integers, fractions, decimals, and percentages. integers are whole numbers that are not written in fractions or decimals. fractions are numbers that are written as a numerator (the top number) and a denominator (the bottom number). decimals are numbers that are written like this: .example 1.23 would be written as .example 1.23, .example .44 would be written as .example 1.23, 4.4 would be written as 4.4, etc. percentages are fractions that have been turned into whole numbers by dividing them by 100%. For example, if someone says they want 3% of something, they would mean
Is √ 4 is a rational number?
√4 is a rational number, meaning that it can be expressed as a fraction.
What is a rational number?
A rational number is a number that can be expressed as a fraction. In other words, it can be divided by another number and the result will be a whole number.
There are two types of rational numbers: positive and negative. Positive rational numbers are the ones that increase as you divide them by another number. Negative rational numbers decrease as you divide them by another number.
What are the properties of Rational Numbers?
The properties of rational numbers are:
1) All irrational numbers are irrational. This means that they cannot be written as fractions or decimals. For example, 2² is not a rational number because it can’t be written as a fraction (2/5). 2³ is also an irrational number because it can’t be written as a decimal (3.1415).
2) Every rational number is between 1 and 2 million (2,000,000) different. This means that there is no two rational numbers that have the same value. For example, 3 is not a rational number because 3 can be written as both 3½ and 3
Is √ 2 is a rational number?
√2 is a rational number. What does that mean? What types of numbers are Rational Numbers? What are their properties?
√2 is a rational number. This means that it can be expressed as a fraction in which the numerator (top number) is equal to the denominator (bottom number). Here is an example:
Here, the numerator (top number) is equal to 3 and the denominator (bottom number) is equal to 2. So, √2 can be expressed as:
3/2 = 1.5
Rational numbers are all numbers that can be expressed as a fraction in which the numerator (top number) is equal to the denominator (bottom number). Here are some other examples:
-1/3 = 0.67
-5/8 = 2.25
-7/16 = 1.68
All of these numbers are rational numbers because they can be written as fractions in which the numerator (top number) equals the denominator (bottom number). Note that there are a few exceptions to this rule – see below for more information on those exceptions.
Is 0.040040004 a rational number?
Rational numbers are numbers that can be expressed as a fraction or decimal.
A rational number is a number that can be expressed as a fraction or decimal. This means that it can be divided into smaller parts and each part still make sense.
There are three types of rational numbers: whole numbers, fractions, and decimals. Whole numbers are the simplest type of rational number and they include numbers like 1, 2, 3, and 4. Fractions are two-part Numbers like 7/10 and 3/5. Decimals are three-part Numbers like .75 and .8.
Rational numbers have some important properties that make them useful in math. One property is that they always have a numerator (the top number) and a denominator (the bottom number). This is known as the LAW OF TRIALS. The numerator always grows by 1 while the denominator stays the same. For example, 3 has a numerator of 3 and a denominator of 10 which makes it a whole number. But 4 has a numerator of 2 and a denominator of 8 which makes it a fraction. And .75 has a numerator of .75 and a denominator of 5 which makes it
Is 1.0227 a rational number?
Rational numbers are numbers that can be expressed as a quotient of two integers.
Rational numbers can be found in many different places in mathematics. They are often used to help solve problems. For example, if you want to figure out how much money you need to buy something, you can use rational numbers to calculate the amount.
There are three main types of rational numbers: whole numbers, fractions, and decimals. Whole numbers are the simplest type of rational number. They are simply integer values that cannot be divided by any other integer value. fractions are rational numbers that are made up of two whole numbers. For example, 2/5 is a fraction because it is made up of two whole numbers (1 and 2). Decimals are rational numbers that are made up of units (like centimeters or millimeters). 1/3 is a decimal because it is made up of threeunits (1, 2, and 3).
There are a few properties of rational numbers that should be familiar by now. First, every rational number has a numerator and a denominator. Second, every rational number is between 0 and 1 (although there are a few exceptions). And finally, every rational number has a decimal representation
Is 0.7777 rational or irrational?
0.777 is a common irrational number. What does that mean and why is it irrational? In this full guide, we’ll explore the definition, types, properties, and examples of irrational numbers. We’ll also explain why they’re considered tricky to work with and why they may be difficult for some students to understand.
So whether you’re looking to learn more about irrational numbers or just want to be sure you don’t confuse them with rational numbers (which are simply whole numbers), this guide is for you!
Is 0.3333 a rational number?
0.3333 is a common fractional value and it is often used in mathematical calculations. However, is it a rational number? In this full guide, we will discuss the definition, types, properties of rational numbers and see if 0.3333 is a rational number.
A rational number is a number that can be expressed as a fraction (i.e. it can be divided into two equal parts). For example, 0.7000 is a rational number because it can be written as 0.7 divided by 1.1416 (note that the numerator and denominator are both fractions).
There are three types of rational numbers: whole numbers, fractions and decimals. A whole number is any number that is not a fraction or decimal (for example, 3). A fraction is a division of one unit of something (for example, 1/2) and a decimal is a division of ten units of something (for example, .75).
0.3333 isn’t a whole number because it’s not divisible by any whole numbers (it’s divisible by .25 but not by .5 or .333). It also isn’t a fraction because it’s not divided into two equal parts
Is 2 √ 3 a rational or irrational number?
Rational numbers are numbers that can be expressed as a quotient of two whole numbers.
There are several types of rational numbers, each with its own properties. In this guide, we’ll explore the definition, types, and properties of rational numbers. We’ll also show you how to convert between them.
We’ll start by defining rational numbers. A rational number is a number that can be expressed as a quotient of two whole numbers. Here’s an example: 2 √ 3 is a rational number because it can be expressed as a quotient of two whole numbers (2 and 3).
There are several types of rational numbers, each with its own properties. We’ll explore the definition, types, and properties of rational numbers in this guide.
Is 7.787887888 a rational number?
If you’re looking for a comprehensive guide to rational numbers, you’ve come to the right place. In this article, we’ll cover the definition of rational numbers, their types, and some of their properties.
First, let’s define what a rational number is. A rational number is a number that can be expressed as a fraction or an equation. For example, 7.787887888 can be expressed as:
7.787887888 = 4 * 3.141592653589793
or
7.787887888 = 8 * 3.141592653589793
Both of these equations are valid expressions for 7.787887888. What this means is that 7.787887888 can be expressed in multiple ways and it still represents the same number. This is important because it means that 7.787887888 is a rational number.
Now that we’ve defined what a rational number is, let’s look at some of their properties. First, all rational numbers are equal (they’re algebraic). Secondly, every rational number has a denominator (i.e., material that goes inside the square brackets in an equation). Lastly, every rational number has a
Is 74.721 rational or irrational?
Rational numbers are numbers that can be expressed as a sum of rational numbers. This means that the numbers can be written in the form a, b, c where a, b, and c are whole numbers.
There are three types of rational numbers: whole numbers, fractions, and decimals. A fraction is a number that is written like this: 3/4. A decimal is a number that is written like this: .75.
Some properties of rational numbers include:
-They have an inverse (if you divide one by the other, they cancel out).
-The sum of two rationals is always a rational (this is called the associative law).
-The cardinality of a set of rationals is equal to the cardinality of the set of whole numbers it includes (this is called the distributive law).
-They are unique (you can’t combine them with any other number).
All these properties make Rational Numbers interesting and useful in many situations. For example, you can use them to calculate square roots and cube roots. You can also find factors and prime factors of irrational numbers using Rational Numbers.
Is pi irrational?
pi is irrational and cannot be represented as a rational number.
This might seem like a strange claim, but it’s true. pi is an irrational number because it cannot be expressed as a rational number, which means that it doesn’t fit into the usual pattern of numbers where each digit can be expressed as a fraction with rational denominator.
Instead, pi consist of infinitely repeating fractions with an infinite denominator. This makes calculation of its value incredibly difficult and there are no known methods for doing so. In fact, the only way to find out the exact value of pi is to perform an infinite calculation!
Is 3.587 rational or irrational?
Rational numbers are numbers that can be expressed as fractions, decimals, and multiples of whole numbers.
A rational number is a number that can be divided into smaller parts without any fractional or irrational parts. For example, 3.587 can be divided into thirds (3/5), fifths (5/10), tenths (10/15), and hundredths (100/125). Every rational number has a certain structure.
There are three types of rational numbers: whole numbers, fractions, and decimals. A whole number is a number that is written without any division symbols (e.g., 3). A fraction is a number that is written with a slash between the numerator and denominator (e.g., 3/5). A decimal is a number that is written with a point above the numeral (e.g., 3.57).
There are many properties of rational numbers that you may be familiar with. For example, every rational number is divisible by at least one whole number and by any integer other than 1 or -1. Every rational number is equal to the sum of its fractions and decimals, except for 0 and 1. And every rational number
Is 3 rational or irrational?
3 is one of the most commonly used numbers in our lives. It’s a basic number we use to describe things like time, distance, and temperature. But is 3 really rational or irrational? And what are its properties?
When we talk about numbers being rational or irrational, we’re referring to their mathematical properties. Numbers that are rational are ones that can be expressed as fractions or decimals. For example, 3 can be expressed as a fraction as 3/5 (meaning three parts out of five). Similarly, 3 can also be represented as a decimal, with the digits 0.33 representing the value of 3.
Numbers that aren’t rational usually don’t have a neat representation like this. For example, 5 can’t be expressed as a fraction or decimal because it doesn’t have a natural division (3/5 and 5/10 are two examples of fractions, but 10/15 and 5/9 aren’t decimals because there’s no number after the 15). In other words, numbers like 5 aren’t rational because they don’t follow the rules of arithmetic (more on this later).
So why do we care about rationality when it comes to numbers? Well, it plays an important role
Is 5 rational or irrational?
What is a rational number?
A rational number is a number that can be expressed as a fraction or decimal. These numbers are often called “rational numbers”, “rational fractions”, or “rational decimals”.
What are the types of rational numbers?
There are three types of rational numbers: whole numbers, fractions, and decimals.
What are the properties of rational numbers?
The properties of rational numbers are as follows:
-They are equal to one another.
-They are commensurable. That is, they can be divided evenly into one another.
-They have a common factor, which is found by multiplying each number by its common divisor (the number that divides both numerator and denominator evenly). For example, the number 6 has a common factor of 2 because it is equal to 2 multiplied by itself six times. The number 12 has a common factor of 1 because it is equal to 1 multiplied by itself twelve times.
-They satisfy the equation x + y = z. In other words, every rational number has a solution (an equation that can be used to find the value of x, y, and z). The solutions to
Is 5 an irrational number?
5 is an irrational number. This means that it cannot be expressed as a rational number, meaning that it cannot be divided by any rational numbers without ending up with a fraction.
There are several reasons why 5 is an irrational number. For example, if you take the square root of 5, you get 1.4142135623730950488. Now, this isn’t a decimal; it’s an irrational number. This is because when you take the square root of anything, you’re going to get something that’s not a rational number.
Another reason 5 is an irrational number is because it can never be expressed as the sum of two rational numbers. For example, if you have two rational numbers, say x and y, then 5 = (x + y) / 2. But there’s no way to write 5 as the sum of two rational numbers!
In general, 5 is an irrational number because it doesn’t obey the laws of arithmetic. However, there are still ways to deal with 5 in mathematical problems.
Is 0.5555 rational or irrational?
Rational numbers are numbers that can be expressed as a fraction.
Rational numbers are defined as those that can be written as a fraction. They include the integers, the rational numbers, and the real numbers.
There are three types of rational numbers: rational fractions, rational decimals, and rational whole numbers.
The simplest type of rational number is a rational fraction. This is a number that can be written as a fraction (e.g. 1/2).
A rational decimal is a number that can be written as a decimal (e.g. .45).
And finally, a rational whole number is a number that can be written as an entire number (e.g. 5).
Rational numbers have many properties that make them useful in mathematics and trigonometry. For example, they are the foundation of modern calculus and are used to solve problems in mathematics and physics.
Is 12.77 rational or irrational?
In this blog post, we are going to learn what is a rational number and what are the different types of rational numbers. We will also look at some properties of rational numbers and see if 12.77 is a rational number.
A Rational Number is a number that can be expressed as a fraction (i.e. a number that consists of parts that can be divided evenly). There are different types of Rational Numbers, and we will look at them in detail in this blog post.
Some common examples of Rational Numbers are: 2, 3, 5, 8, 10, 12 etc.
12.77 is not a Rational Number because it cannot be expressed as a fraction.
Is 0.692 rational or irrational?
0.692 is an irrational number. This means that there is no rational number that is equal to 0.692. In other words, it’s impossible to find a rational number that is two thirds of 0.692.
0.692 can also be called a square root of -1, because it’s the square root of the number -1 that’s not a square. The other two square roots of -1 are 1 and 1.5236, so 0.692 is in between them.
0.692 is a decimal expansion, which means that it continues to increase as you add more zeroes to the end. For example, 0.6920571… would be an expanded version of 0.692.
Is 6.24 a rational number?
What is a rational number?
A rational number is a number that can be expressed as a fraction or decimal.
There are a few types of rational numbers: whole numbers, decimals, percents, and fractions.
Whole numbers are the simplest type of rational number. A whole number is just a number that is written without any commas or fractions. For example, 6.24 is a whole number because it can be written as 6 and .24.
Decimals are another type of rational number. A decimal is a number that is written with periods ( . ). For example, 6.24 is a decimal because it can be written as 6.24, 0.64, and .084.
Percents are another type of rational number. A percent is just a fraction with 100% added at the end (%). So, 6.24% would be written as 6 24/100 or 6%.
Fractions are the last type of rational numbers. A fraction is just two whole numbers separated by a slash (/.). For example, 3/5 would be written as 3 5/10 or 30%.
Now that you understand what a
Is 0.101100101010 an irrational number?
Rational numbers are a type of number that can be expressed using a rational equation. This means that the number can be broken down into smaller parts, and each part can be expressed as a rational number.
There are a few different types of rational numbers. The most common type is the rational number. This is a number that can be expressed as a proportion or an equation. For example, 0.101100101010 can be expressed as a proportion, which means that it is 10/100th of a whole number. Alternatively, it can be expressed as an equation, which means that it is 10x+1.
Another type of rational number is the fractional rational number. This is a number that can be expressed as a fraction, such as 1/4 or 3/8. Fractional rational numbers are important because they have properties that are different from other types of rational numbers. For example, 1/4 is two thirds of a whole number, but 3/8 is three fifths of a whole number.
There are also special types of irrational numbers called transcendental numbers. These are numbers that cannot be expressed using any equations or proportions. Examples include pi (3.141592653589793
Is 1.3333 a rational number?
1.3333 is a common and unusual number. It is an integer, but it also has a fractional component. It is called a rational number because it can be expressed as a fraction (1/3).
There are several types of rational numbers: whole numbers, decimal numbers, fractions, irrational numbers, and transcendental numbers.
Whole numbers are the numbers that are written as 1, 2, 3, 4, 5, 6…etc. Decimal numbers are the ones that end in .pdf or .xyz. Fractions are the numbers that are written like 1/2, 3/4, and 5/6. Irrational numbers are the ones that don’t have a rational counterpart (e.g., Pi). Transcendental numbers are the ones that can’t be expressed as a rational number (e.g., √2).
Properties of rational numbers include:
-They can be multiplied together to create larger whole or decimal numbers
-They can be divided equally by any other whole or decimal number
-They can be raised to any power and remain a rational number
Is 3.275 rational or irrational?
Rational numbers are numbers that can be written in the form a/b, where a and b are integers. There are several different types of rational numbers, each with its own properties.
In this guide, we’ll explore the definition of rational numbers, their types, and some of their properties. We’ll also look at an example that shows how irrational numbers can be written in the form a/b.
So let’s start by taking a look at the definition of a rational number: a rational number is a number that can be written in the form a/b, where a and b are integers. This means that all of the factors (a, b, c, etc.) must be evenly divisible by b.
Next, let’s take a look at the different types of rational numbers. There are two main types of rational numbers: whole numbers and fractions. Whole numbers are just like regular old integers except they have a fractional component too (e.g. 3.75). Fractions are just like regular decimals except there’s an integer component too (e.g. .5).
Finally, we’ll look at some of the properties of rational numbers. For example, rational numbers
Is 0.95929409956639 rational or irrational?
0.95929409956639 is a rational number. This means that it can be expressed as a quotient of two rational numbers.
The most common way to express 0.95929409956639 is as a fraction, which is 0.5929409956639 / 0.95929409956639. This fraction can be seen on the left side of the following equation:
0.95929409956639 = 0.59294 / 0.959294
This fraction is known as a rational fraction because it can be written in the form q / r, where q and r are whole numbers and q ≠ 0.rationality means that this fraction cannot be expressed as the quotient of two irrational numbers (ie numbers that cannot be expressed as the quotient of two rational numbers).
0.95929409956639 is also a rational square root because it can be written as:
0.95929409956639 = √(0.52592949923907)
This Rational Square Root can be seen on the right side of the following equation:
0.9
Is 8876546 rational or irrational?
Rational numbers are numbers that can be expressed as a fraction or decimal.
There are many types of rational numbers, including whole numbers, fractions, and decimals.
What is the difference between a fraction and a decimal?
A fraction is a number that is written as a division of two whole numbers. For example, 4/9 is a fraction because it is written as the division of 4 by 9. The numerator (top number) is 4 and the denominator (bottom number) is 9.
A decimal is a number that is written as the division of two whole numbers. For example, 8.7 is a decimal because it is written as the division of 8 by 10. The numerator (top number) is 8 and the denominator (bottom number) is 10.
Is 0.6666 rational or irrational?
Rational numbers are numbers that can be expressed as a fraction, such as 0.6666.
Rational numbers are special because they have some properties that are not shared by other types of numbers. For instance, a rational number can be expressed as a fraction, and its numerator and denominator can both be rational numbers.
There are several different types of rational numbers, including whole numbers, fractions, decimals, and percents. Each type of rational number has its own specific properties.
For example, fractions are special because they can be written in two different ways: as numerators and denominators, or as a numerator and a denominator with a slash between them. This allows fractions to be divided evenly (and smoothly) between two numbers.
Similarly, decimals can be expressed in two ways: as a decimal number and as the sum of consecutive whole numbers. This makes it easy to compare decimals without having to convert them into degrees or radians.
Lastly, percents can be written in various ways: as the percent of something (like income), the percent of something multiplied by 100 (to make it easier to read), or the percent sign followed by a
Is √ 3 an irrational number?
√ 3 is an irrational number because it cannot be expressed as a rational number.
√ 3 is an irrational number because it cannot be expressed as a rational number. There are several different types of irrational numbers, and √ 3 is one of them.
There are several different types of irrational numbers, and √ 3 is one of them. √ 3 is also known as an indeterminate exponential number. This means that it has no clear terminating pattern or sequence, which makes it difficult to understand or work with.
This means that it has no clear terminating pattern or sequence, which makes it difficult to understand or work with. √ 3 also has properties that are different from other irrational numbers. For example, √ 3 always equals 1.6180339887495. This is called the fundamental theorem of algebra and it holds true for all irrational numbers, including √ 3.
Is 10 an irrational number?
Rational numbers are numbers that can be expressed as a quotient of two whole numbers. They include the numbers between 1 and 10 as well as the fractions 2/5, 3/8, and 1/3.
There are several different types of rational numbers, including whole number rationals, fractional rationals, decimal rationals, and mixed fractional-decimal rationals.
Each type of rational number has its own specific properties. For example, whole number Rationals can be added, subtracted, multiplied, and divided by each other without changing their value. Fractional rationals also have this same property, but they also have a fractional component. Mixed fractional-decimalrationals have both a fractional and a decimal component.
All rational numbers are equal in magnitude (they have the same size), but they may not be equal in value (they may be different multiples of each other).